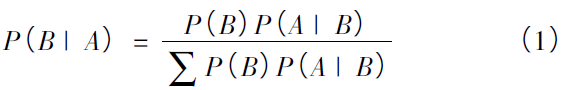数控机床电气驱动系统可靠性研究

　数控机床作为现代制造业的基础设备，被认为是集合多门学科的产物。在数控机床中，电气控制作为其关键的部分，对数控机床的运行具有极其重要的作用。通过控制系统让各个部件能够协调运作，并共同完成加工任务。因此，在机床的设计中，提高机床电气系统的可靠性，成为各国提高机床质量、增强市场竞争力的先决条件。本文结合电气控制系统的原理及构成，提出一种基于故障树的系统可靠性检验方法，并对其的实现进行了具体分析。
1 数控车床电控驱动系统原理及构成
本研究以某数控重型卧式车床为例，其控制系统为西门子840D 数控系统。数控车床的结构如图1 所示，包括床身、尾座、主电机等。该车床主要用于对盘类和轴类等回转体零件进行加工，可自动完成锥面、圆弧面、切槽等的加工，具有精度高、应用范围广等特点。
该车床电控驱动系统是其核心部分，控制车床各个部件协调工作，并完成加工任务。结合该车床的结构，其电控驱动系统的功能具体如图2 所示。

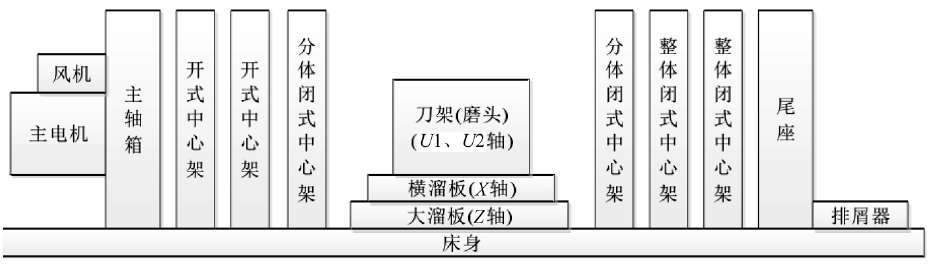
图1 某数控车床的组成

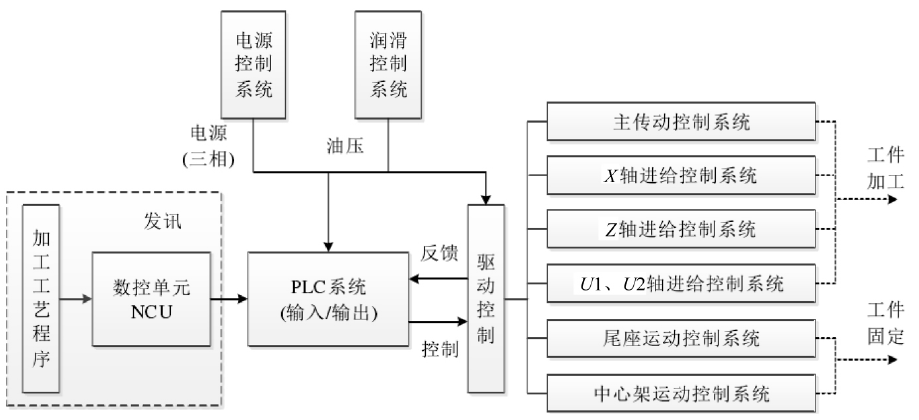
图2 电气控制与驱动系统功能组成
2 系统可靠性建模
2． 1 可靠性框图建立
在对系统的可靠性进行分析前，必须要对系统进行可靠性建模。而可靠性建模主要描述各个子系统、零部件等对整个系统的影响，进而反映产品的失效规律。对此，结合图2 的电控驱动系统，选择主传动系统构架可靠性模型，并借助故障树建模，对其失效规律进行研究。其主要包括系统功能框图和系统可靠性框图两个部分。
1) 系统功能框图。
功能框图是建立可靠性模型的前提，并从结构层次和功能层次的角度，反映出内部不同单元之间的关系。参照主传动系统的结构和工作原理，可得到其功能框图，具体如图3 所示。图中左半部分为系统的功能介绍，右半部分为系统的基本组成。

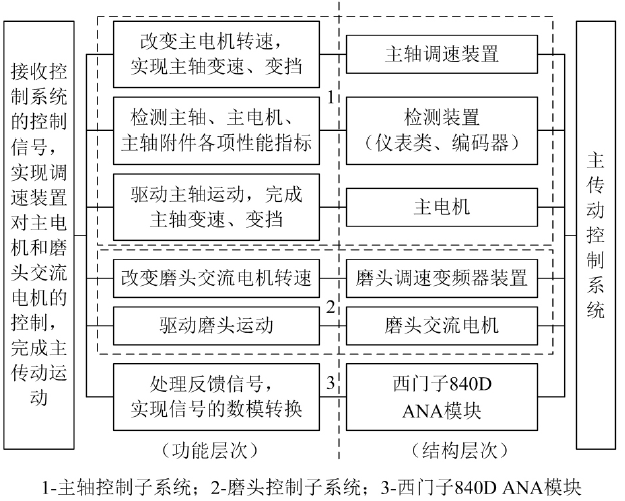
图3 主传动控制系统功能框图
2) 系统可靠性框图。
可靠性框图主要是结合系统的逻辑结构，从可靠性的角度表达不同组成单元之间运行的关系。而通过图3 所示的系统功能框图，可以知道组成该系统的电气部件都具备正常、故障和降级3种不同的状态。因此，本研究提出建立多态可靠性框图。在可靠性框图中，对电气元件的功能状态采用0，0． 5 和1 进行描述，上述数值分别表示正常、降低和故障3 种状态，具体如图4 所示。
2． 2 主传动控制系统故障树建立
根据故障树建模原理，同时结合主传动系统的构成，以主传动系统中的主轴控制系统为例，建立如图5 所示的主故障树。而以主轴控制系统为例，是因为该部分是主传动系统的核心。
根据电气元件的运行状态，并结合专家经验、故障程度以及实际调研的数据进行分析，可以得到

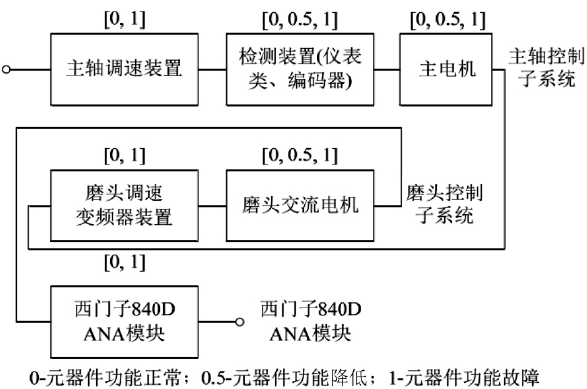
图4 主传动控制系统多态可靠性框图

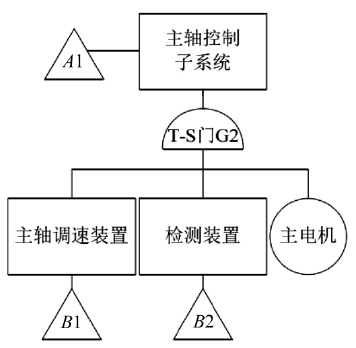
图5 主轴控制系统主故障树
主轴控制系统所具备的多种状态，以及不同状态所产生的故障类型。换句话说，不同的状态是导致电气元件功能下降还是会导致故障，都有其可能性，是不确定的，并且各种可能性都存在一定的概率。如电动机动力不足，那么导致上层事件功能降低的概率可达到0． 8，而出现功能故障的可能性则为0． 2。因此，必须要对图5 中的T － S 门G2的逻辑规则进行定义，具体的定义见表1。

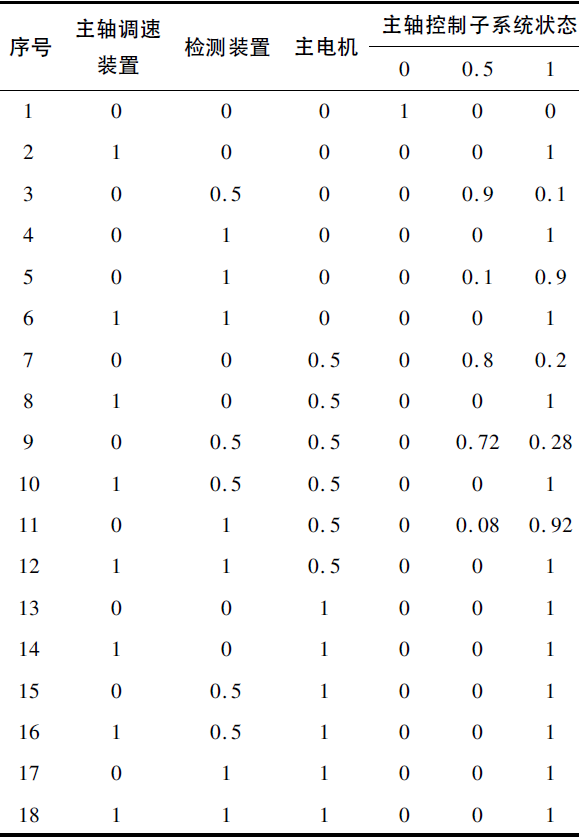
表1 T － S 门G2 规则设计
根据图5 所示的主轴子系统主树，采用自上而下的方式对故障进行梳理，可以得到各个时间产生故障的原因，以及各个部件产生的故障模式。
如主轴调速装置可能出现两种不同的状态，即正常和故障，当其出现故障的时候，其表现往往为控制失效，因此可以从控制失效的两个主要原因——“工作失效”和“供电失效”入手，建立主轴调速装置控制失效故障树子树，如图6 所示。

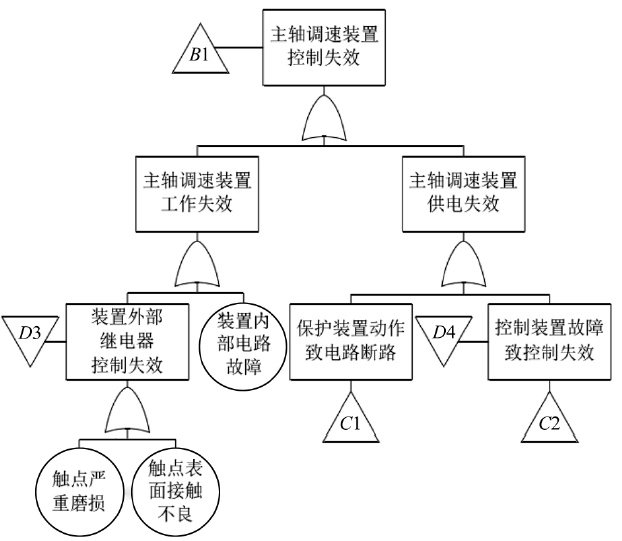
图6 主轴调速装置控制失效故障树子树
3 基于贝叶斯模型的故障树建立
3． 1 贝叶斯网络原理
上述故障树模型需要对其进行求解，从而计算出不同子树下设备的失效概率，因此本文引入贝叶斯网络模型。贝叶斯网络主要由节点和有向边组成，通常被称作基于概率推理的有向无环图。
在图中，节点表示一种随机变量，而有向边则主要连接各个节点，并表示出不同节点之间的关系。一般情况下，根节点无父节点，此时用先验概率来进行表达，而叶节点无子节点，子节点的关系强度则用条件概率来表达。因此，贝叶斯网络通常用于描述设备故障原因的不确定性及关联性。用概率进行描述，则为: 若已知随机变量A 和B，在已知节点A 的状态下，节点B 处于某种状态的概率可以表示为

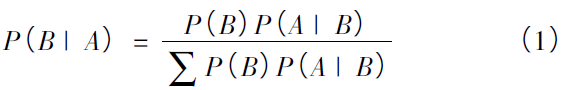
式中: P( B | A) 为节点B 的条件概率; P( B) 为节点B 的先验概率; P( A | B) 为节点A 的条件概率。
3． 2 主轴控制子系统故障树定量分析
将图5 所示的主故障树向贝叶斯网络转化，具体方法是通过与门、或门、优先与门以及冷备件门的失效机理，得到对应的贝叶斯网络。以与门为例，令X = ［X1，X2，…，Xm］，其中m 为与门底事件的个数，令Y 为与门时间的输出变量，根据与门的失效机理，可以得到Y 的条件分布概率:

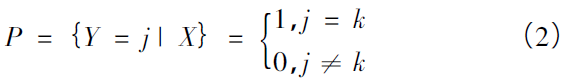
由此，与门对应的贝叶斯网络如图7 所示。

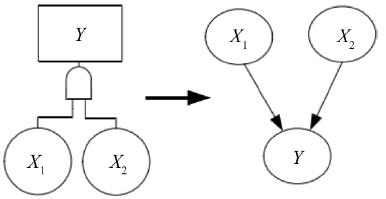
图7 与门及对应的贝叶斯网络

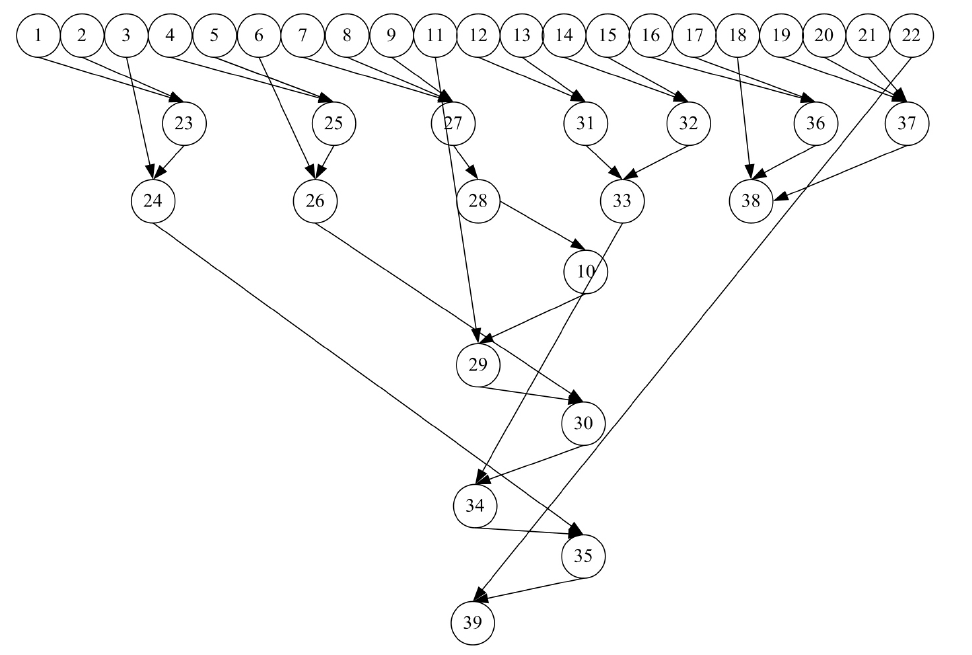
图8 主轴控制子系统贝叶斯网络
根据图7 所示的原理，将主轴控制系统的故障树转化为图8 所示的贝叶斯网络。
3． 3 主传动控制系统可靠性评估
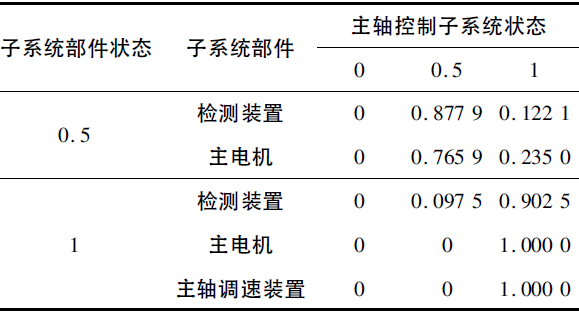
结合贝叶斯网络的双向推理理论，对主轴控制子系统进行自上而下的因果推理，从而得到其不同部件的重要程度，具体结果见表2。
4 结束语
本文针对电气驱动控制系统的复杂性、多态性和模糊性等特点，利用故障树方法对可靠性进行建模，并基于贝叶斯网络对模型进行定量分析，最终完成对电控系统中主轴控制部分的可靠性评估。
通过评估，得到主轴控制系统中不同组件的重要程度: 当子系统的部件状态在降低时，如果主轴控制系统状态也在降低，则检测装置发生故障的概率为0． 877 9; 同样，当子系统部件出现故障同时主轴控制系统也出现故障时，其故障主要来源于主电机。上述故障判断方法的应用，可为数控机床电气驱动系统的可靠性运行提供帮助。